グラフからわかる等角写像（美しき数学の世界）

　数式が描く綺麗な曲線の軌跡に魅せられる。数学の楽しみの一つです。
　碁盤の目のような直交する直線群が正則関数（ある領域において複素微分可能な複素数を変数に持つ複素数値関数）により、どのような曲線群に変換されるのか大変興味があるところではないかと思います。
　実は、正則関数は複素微分の値がゼロにならない全ての点で、等角写像になることが知られています。
　このブログでは、初等的な複素数値関数をいくつか例に挙げ、その関数の等角写像のグラフを表示します。
　このグラフを読めば初等的な複素数値関数の等角写像のグラフが、どのような曲線の軌跡を描くのかがわかるでしょう。

等角写像とは：
複素平面から複素平面への写像$ \ f \ $が$ \ ( x_{ 0 }, y_{ 0 } ) \ $において等角写像( conformal transformation)であるとは、点$ \ ( x_{ 0 }, y_{ 0 } ) \ $において交差し、かつ接線を持つ二つの曲線を$ \ C_{ 1 }, C_{ 2 } \ $とするとき、曲線の像$ \ f( C_{ 1 } ), \ f( C_{ 2 } ) \ $は点$ \ ( \ f( x_{ 0 } ), \ f( y_{ 0 } ) \ ) \ $において交差し、かつ接線を持ち、複素平面上の二曲線の交角は写像$ \ f \ $によっても等しく保たれるような写像のことをいう。

準備
$f(z)=z^{2} \ $のグラフ
$\displaystyle f(z) = \frac{ 1 }{ z } \ $のグラフ
$f(z) = \exp z$のグラフ
まとめ

準備

　最初に碁盤の目のような互いに直交する直線の群を作成します。ｘ軸／ｙ軸それぞれ最小値を$ \ -1.00 \ $とし、最大値$ \ +1.00 \ $まで$ \ 0.1 \ $間隔で直線を引きます.

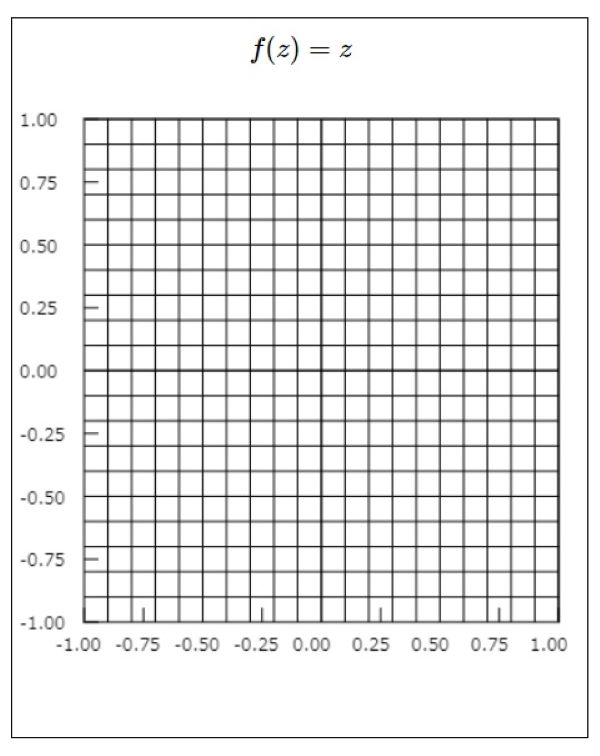
この碁盤の目のような直線群が正則関数により、どのようなグラフに変換されるのかを見て行きます。

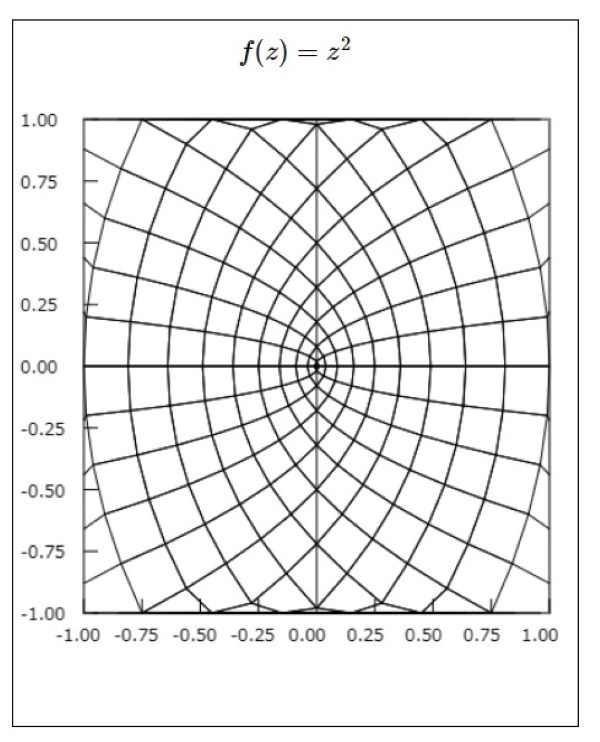
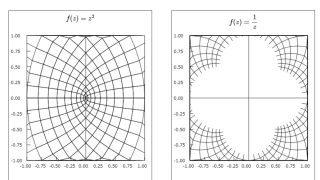
$f(z)=z^{2} \ $のグラフ

複素数$ z = x + \sqrt{-1} \cdot y $に対して$ f(z) = z^{2} $の実数部と虚数部を求めると

\[
\begin{align*}
f(z)
= f(x + \sqrt{-1} \cdot y)
= (x + \sqrt{-1} \cdot y)^{2}
= (x^{2} – y^{2}) + \sqrt{-1} \cdot (2 x y)
\end{align*}
\]
となります.したがって
\[
\Re( z^{2} ) = x^{2} – y^{2} \qquad \Im( z^{2} ) = 2 x y
\]
となります.そこで横軸に実数部,縦軸に虚数部をプロットすれば次の様なグラフになります.

複素解析　1変数解析関数（ちくま学芸文庫） [ 笠原乾吉 ]

価格:1,430円
(2023/3/5 16:33時点)
感想(0件)

JavaScriptコードレシピ集スグに使えるテクニック278　最新ECMAScri [ 池田泰延 ]

価格:3,278円
(2023/3/5 16:36時点)
感想(0件)

$\displaystyle f(z) = \frac{ 1 }{ z } \ $のグラフ

複素数$z = x + \sqrt{-1} \cdot y$とおいて$\displaystyle f(z) = \frac{ 1 }{ z } \ $の実数部と虚数部を求めると

\[
\begin{align*}
f(z)
= f( x + \sqrt{-1} \cdot y )
= \frac{1}{x + \sqrt{-1} \cdot y }
&= \frac{x \ – \ \sqrt{-1} \cdot y}{(x + \sqrt{-1} \cdot y)(x \ – \ \sqrt{-1} \cdot y)}
\\
&= \frac{x \ – \ \sqrt{-1} \cdot y}{x^{2} + y^{2}}
\\
&= \left ( \frac{x}{x^{2} + y^{2}} \right ) + \sqrt{-1} \cdot \left ( – \ \frac{y}{x^{2} + y^{2}} \right )
\end{align*}
\]
となります.したがって
\[
\Re \left ( \frac{ 1 }{ z } \right ) = \frac{ x }{ x^{2} + y^{2} } \quad
\Im \left ( \frac{ 1 }{ z } \right ) = – \ \frac{ y }{ x^{2} + y^{2} }
\]
となります.そこで横軸に実数部,縦軸に虚数部をプロットすれば次の様なグラフになります.

$f(z) = \exp z$のグラフ

オイラーの公式(Euler’ formula)により,任意の複素数$ z $に対して
\[
\exp \sqrt{-1} \cdot z = \cos z + \sqrt{-1} \cdot \sin z
\]
となることに注意して.複素数$ z = x + \sqrt{-1} \cdot y $とおいて$ f( z ) = \exp z $の実数部と虚数部を求めると
\[
\begin{align*}
f(z)
= f(x + \sqrt{-1} \cdot y)
= \exp(x + \sqrt{-1} \cdot y)
&= \exp x \exp \sqrt{-1} \cdot y
\\
&= \exp x ( \cos y + \sqrt{-1} \cdot \sin y )
\\
&= \exp x \cos x + \sqrt{-1} \cdot \exp x \sin y
\end{align*}
\]
となります.したがって
\[
\Re( \exp z ) = \exp x \cos y , \quad
\Im( \exp z ) = \exp x \sin y
\]
となります.そこで横軸に実数部,縦軸に虚数部をプロットすれば次の様なグラフになります.

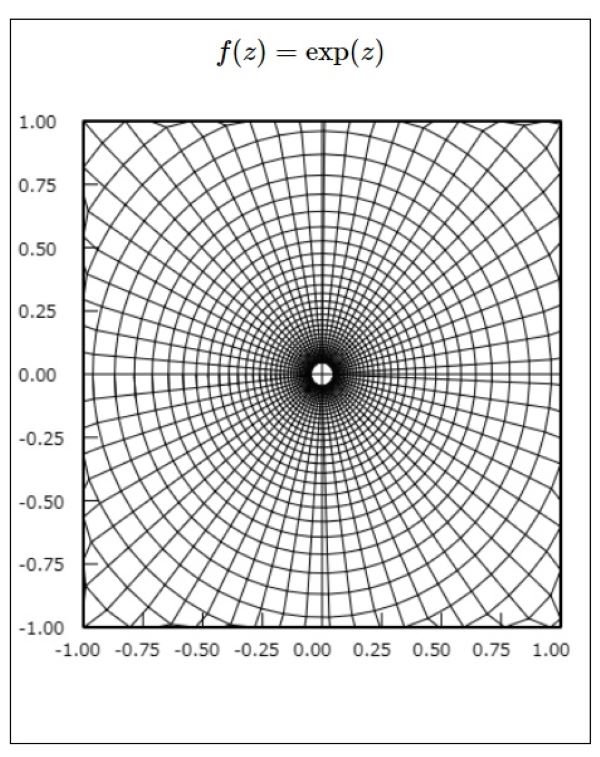
但し、このグラフの原像の範囲は$x$軸、$y$軸それぞれ最小値を$ \ – \ 3.14 \ $最大値を$ \ 3.14 \ $としました.

JavaScriptコードレシピ集スグに使えるテクニック278　最新ECMAScri [ 池田泰延 ]

価格:3,278円
(2023/3/5 16:36時点)
感想(0件)

複素解析　1変数解析関数（ちくま学芸文庫） [ 笠原乾吉 ]

価格:1,430円
(2023/3/5 16:33時点)
感想(0件)

まとめ

　今回のブログでは、最も基本的な複素関数の等角写像のグラフを描いてみました。このグラフはHTMLのCANVAS要素を使用して javascript でプログラムを作りました。また、このブログに載っている数式はMarkdown記法により書いてあります。数式の書き方については、こちらのブログ「ワードプレスで数式を」をご覧ください。