「ヤコビ行列とは何か」ご存知でしょうか?微積分やベクトル解析の教科書に載っている行列を丸暗記するだけで済ましてはいませんか?
ヤコビ行列は、微分するという線形変換(微分演算子)の標準基底に関する表現行列です。有限次元の線形変換は、基底により行列の形で表現することが可能です。
「ヒルベルト空間上の線形作用素論」を学んだ学生時代の記憶を辿りながら、ヤコビ行列に関する記事をドキュメントにしました。
この記事で解説するヤコビ行列は2×2の行列のみです。簡単な線形代数と微分、偏微分の知識があれば読める内容になっています。
この記事を読むとヤコビ行列について、より一層の理解を深めることができると思います。
これからベクトル解析や解析力学などを学ばれる方々にとって、少しでもお役に立てれば光栄です。
この記事では二次元ユークリッド空間\( \mathbb{ R }^{ 2 } \ \)の元を列ベクトルで
\[
\begin{pmatrix} \xi_{ 1 } \\ \xi_{ 2 } \end{pmatrix} \in \mathbb{ R }^{ 2 }
\]
と記述することにします。
二次元ユークリッド空間の線形変換
このセクションでは二次元ユークリッド空間上の線形変換を定義し、例として行列について扱います。
いま \( T \) が\( \mathbb{ R }^{ 2 } \ \)から\( \mathbb{ R }^{ 2 } \ \)への写像(maping)であるとは、任意の元\(\begin{pmatrix} \xi_{ 1 } \\ \xi_{ 2 } \end{pmatrix} \in \mathbb{ R }^{ 2 } \)に対して、ただ一つの\( \mathbb{ R }^{ 2 } \ \)の元が対応することである。このとき
\[
T \begin{pmatrix} \xi_{ 1 } \\ \xi_{ 2 } \end{pmatrix} \in \mathbb{ R }^{ 2 }
\]
と記述します。
定義(線形変換)
\( \mathbb{ R }^{2} \)から\( \mathbb{ R }^{2} \)への写像 \( T \)が次の二つの条件を満たすとき写像\( T \)を線形変換( linear transformation )という
1:任意の\(\begin{pmatrix} \xi_{1} \\ \xi_{2} \end{pmatrix}, \ \begin{pmatrix} \eta_{1} \\ \eta_{2} \end{pmatrix} \in \mathbb{ R }^{2} \)に対して
\[
T \left ( \begin{pmatrix} \xi_{1} \\ \xi_{2} \end{pmatrix} + \begin{pmatrix} \eta_{1} \\ \eta_{2} \end{pmatrix} \right ) = T \begin{pmatrix} \xi_{1} \\ \xi_{2} \end{pmatrix} + T \begin{pmatrix} \eta_{1} \\ \eta_{2} \end{pmatrix}
\]
が成り立つ.
2:任意の\( \begin{pmatrix} \xi_{1} \\ \xi_{2} \end{pmatrix} \in \mathbb{ R }^{ 2 }, \ \alpha \in \mathbb{ R } \)に対して
\[
T \left ( \alpha \begin{pmatrix} \xi_{1} \\ \xi_{2} \end{pmatrix} \right )
= \alpha \left ( T \begin{pmatrix} \xi_{1} \\ \xi_{2} \end{pmatrix} \right )
\]
が成り立つ.
例(二次元の線形変換の例)
行列
\[
\begin{pmatrix}
a_{11} & a_{12} \\ a_{21} & a_{22}
\end{pmatrix}
\]
を用いて線形変換\( T \)を
\[
T \begin{pmatrix} \xi_{1} \\ \xi_{2 } \end{pmatrix} =
\begin{pmatrix}
a_{11} & a_{12} \\ a_{21} & a_{22}
\end{pmatrix}
\begin{pmatrix} \xi_{1} \\ \xi_{2 } \end{pmatrix} =
\begin{pmatrix} a_{11} \xi_{1} + a_{12} \xi_{2} \\ a_{21} \xi_{1} + a_{22} \xi_{2 } \end{pmatrix}
\in \mathbb{ R }^{2}
\]
と定義するとき\( T \)は\( \mathbb{ R }^{2} \)から\( \mathbb{ R }^{2} \)への線形変換になる.
証明に関してはこちらを参照して下さい。
線形変換の表現行列
このセクションでは \( \mathbb{ R }^{2} \)の標準基底
\[
\left \{ \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \quad \begin{pmatrix} 0 \\ 1 \end{pmatrix} \right \}
\]
に関する線形変換 \( T \)の表現行列を定義します。任意の\( \begin{pmatrix} \xi_{1} \\ \xi_{2} \end{pmatrix} \in \mathbb{ R }^{2} \)に対して
\[
T \begin{pmatrix} \xi_{1} \\ \xi_{2} \end{pmatrix} = T \left ( \xi_{1} \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \xi_{2} \begin{pmatrix} 0 \\ 1 \end{pmatrix} \right ) = \xi_{1} T \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \xi_{2} \begin{pmatrix} 0 \\ 1 \end{pmatrix}
\]
が成り立つ.このとき線形変換\( T \)は\( \, \mathbb{ R }^{2} \, \)から\( \, \mathbb{ R }^{2} \, \)への写像だから
\[
T \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} a_{11} \\ a_{12} \end{pmatrix}, \quad T \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} a_{21} \\ a_{22} \end{pmatrix}
\]
を満たす\( \, \begin{pmatrix} a_{11} \\ a_{12} \end{pmatrix}, \ \begin{pmatrix} a_{21} \\ a_{22} \end{pmatrix} \in \mathbb{ R }^{2} \, \)が必ず存在するから
\[
\begin{align*}
T \begin{pmatrix} \xi_{1} \\ \xi_{2} \end{pmatrix} = \xi_{1} T \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \xi_{2} T \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \xi_{1} \begin{pmatrix} a_{11} \\ a_{12} \end{pmatrix} + \xi_{2} \begin{pmatrix} a_{21} \\ a_{22} \end{pmatrix} & = \begin{pmatrix} \xi_{1} a_{11} \\ \xi_{1} a_{12} \end{pmatrix} + \begin{pmatrix} \xi_{2} a_{21} \\ \xi_{2} a_{22} \end{pmatrix}
\\ & = \begin{pmatrix} a_{11} \xi_{1} \\ a_{12} \xi_{1} \end{pmatrix} + \begin{pmatrix} a_{21} \xi_{2} \\ a_{22} \xi_{2} \end{pmatrix}
\\ & = \begin{pmatrix} a_{11} \xi_{1} + a_{21} \xi_{2} \\ a_{12} \xi_{1 } + a_{22} \xi_{2} \end{pmatrix}
\end{align*}
\]
が成り立つ.ここで
\[
\begin{pmatrix} a_{11} \xi_{1} + a_{21} \xi_{2} \\ a_{12} \xi_{1 } + a_{22} \xi_{2} \end{pmatrix} = \begin{pmatrix} a_{11} & a_{21} \\ a_{12} & a_{22} \end{pmatrix} \begin{pmatrix} \xi_{1} \\ \xi_{2} \end{pmatrix}
\]
と定義(規約)すれば
\[
T \begin{pmatrix} \xi_{1} \\ \xi_{2} \end{pmatrix} = \begin{pmatrix} a_{11} & a_{21} \\ a_{12} & a_{22} \end{pmatrix} \begin{pmatrix} \xi_{1} \\ \xi_{2} \end{pmatrix}
\]
が成り立つ.この行列
\[
\begin{pmatrix} a_{11} & a_{21} \\ a_{12} & a_{22} \end{pmatrix}
\]
を線形変換\( T \)の標準基底に関する表現行列という.
微分可能性
このセクションでは、\( \mathbb{ R }^{2} \, \)の上に値をとる二変数関数
\[
F ( x, y ) = \begin{pmatrix} f( x, y ) \\ g( x, y ) \end{pmatrix} \in \mathbb{ R }^{2}
\]
の微分可能性を定義します.ただし \( f( x, y ), \, g( x, y ) \)はそれぞれ \( \, \mathbb{ R }^{2} \, \)から\( \, \mathbb{ R } \, \)への二変数関数とします.
その前に一変数関数の微分可能性について復習しておきます.
一変数関数 \( f : \mathbb{ R } \to \mathbb{ R } \, \)が\( x_{0} \in \mathbb{ R } \)において微分可能であるとは
\[
\lim_{ x \to x_{0} } \frac{ f( x ) \ – \ f( x_{0} ) }{ x \ – \ x_{0} } = \alpha
\]
を満たす \( \, \alpha \in \mathbb{ R } \, \)が存在することである.このとき
\[
\alpha = \frac{ d f }{ d x } ( x_{0} )
\]
と記述する.
これをε-δ論法を用いて書き直すと
任意の\( \, \varepsilon > 0 \, \)に対して,ある\( \, \delta > 0 \, \)が存在して
\[
\left | x \ – x_{0} \ \right | < \delta \quad \text{ならば} \quad \left | \frac{ 1 }{ x \ – \ x_{0} } \left ( f( x ) \ – f( x_{0} ) \ – \ \alpha ( x \ – \ x_{0} ) \right ) \right | < \varepsilon
\]
を満たす\( \, \alpha \in \mathbb{ R } \, \)が存在することである.ただし
\[
\frac{ f( x ) \ – \ f( x_{0} ) }{ x \ – \ x_{0} } \ – \ \alpha = \frac{ 1 }{ x \ – \ x_{0} } \left ( f( x ) \ – \ f( x_{0} ) \ – \ \alpha ( x \ – \ x_{0} ) \right )
\]
と変形できることに注意していただきたい.ここで,もう一つ注意すべきことは任意の \( \, \alpha \in \mathbb{ R } \, \)を固定したとき
\[
T ( x ) = \alpha x \quad x \in \mathbb{ R }
\]
と定義すれば, \( \, T \, \)は \( \, \mathbb{ R } \, \) から \( \, \mathbb{ R } \, \)への線形変換になるということです.
この一変数関数の微分可能性の定義を二変数関数に拡張すると次の様になります.
定義(二変数関数の微分可能性)
\( \mathbb{ R }^{2} \)の上に値を取る二変数関数
\[
F( x, y ) = \begin{pmatrix} f( x, y ) \\ g( x, y ) \end{pmatrix} \in \mathbb{ R }^{2}
\]
が \( ( x_{0}, y_{0} ) \in \mathbb{ R }^{2} \, \)において微分可能であるとは,任意の\( \varepsilon > 0 \)に対して,ある\( \delta > 0 \)が存在して
\[
\sqrt{ ( x – x_{0} )^{2} + ( y – y_{0} )^{2} } < \delta
\]
ならば
\[
\left | \frac{1}{\sqrt{ ( x \ – \ x_{0} )^{2} + ( y \ – \ y_{0} )^{2} }} \left ( \begin{pmatrix} f( x, y ) \\ g( x, y ) \end{pmatrix} \ – \ \begin{pmatrix} f( x_{0}, y_{0} ) \\ g( x_{0}, y_{0} ) \end{pmatrix} \ – \ DF \begin{pmatrix} x \ – \ x_{0} \\ y \ – \ y_{0} \end{pmatrix} \right ) \right | < \varepsilon
\]
を満たす線形変換\( \, DF \, \)が存在することである.
ヤコビ行列
ここで偏微分について説明する必要があります.
いま\( \, f( x, y ) \, \)を\( \, \mathbb{ R }^{2} \, \)から\( \, \mathbb{ R } \, \)への二変数関数とするとき
\( \, f( x, y ) \, \)が\( \, \begin{pmatrix} x_{0} \\ y_{0} \end{pmatrix} \in \mathbb{ R }^{2} \, \)において\( \, x- \, \)方向に偏微分可能であるとは,任意の\( \, \varepsilon > 0 \, \)に対して,ある\( \, \delta > 0 \, \)が存在して
\[
| x \ – \ x_{0} | < \delta \quad \text{ならば} \quad \left | \frac{1}{ x \ – \ x_{0} } \left ( f( x, y_{0} ) \ – \ f( x_{0}, y_{0} ) \ – \ \alpha ( x \ – \ x_{0} ) \right ) \right | < \varepsilon
\]
を満たす\( \, \alpha \in \mathbb{ R } \, \)が存在することである.このとき
\[
\alpha = \frac{ \partial f }{ \partial x } ( x_{0}, y_{0} )
\]
と記述します.
\( \, f( x, y ) \, \)が\( \, \begin{pmatrix} x_{0} \\ y_{0} \end{pmatrix} \in \mathbb{ R }^{2} \, \)において\( \, y- \, \)方向に偏微分可能であるとは,任意の\( \, \varepsilon > 0 \, \)に対して,ある\( \, \delta > 0 \, \)が存在して
\[
| y \ – \ y_{0} | < \delta \quad \text{ならば} \quad \left | \frac{1}{ y \ – \ y_{0} } \left ( f( x_{0}, y ) \ – \ f( x_{0}, y_{0} ) \ – \ \beta ( y \ – \ y_{0} ) \right ) \right | < \varepsilon
\]
を満たす\( \, \beta \in \mathbb{ R } \, \)が存在することである.このとき
\[
\beta = \frac{ \partial f }{ \partial y } ( x_{0}, y_{0} )
\]
と記述します.
定理(ヤコビ行列)
\( \mathbb{ R }^{2} \)の上に値をとる二変数関数
\[
F( x, y ) = \begin{pmatrix} f( x, y ) \\ g( x, y ) \end{pmatrix} \in \mathbb{ R }^{2}
\]
が \( \, \begin{pmatrix} x_{0} \\ y_{0} \end{pmatrix} \in \mathbb{ R }^{2} \, \)において微分可能ならば, \( \, f( x, y ), \, g( x, y ) \, \)は\( \, \begin{pmatrix} x_{0} \\ y_{0} \end{pmatrix} \in \mathbb{ R }^{2} \, \)において\( \, x-, \, y- \, \)方向にそれぞれ偏微分可能で, \( \, F \, \)の微分に関する線形変換を\( \, DF \, \)とするとき
\[
DF \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} \frac{ \partial f }{ \partial x } ( x_{0}, y_{0} ) \\ \frac{ \partial g }{ \partial x } ( x_{0}, y_{0} ) \end{pmatrix}, \quad DF \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} \frac{ \partial f }{ \partial y } ( x_{0}, y_{0} ) \\ \frac{ \partial g }{ \partial y } ( x_{0}, y_{0} ) \end{pmatrix}
\]
が成り立つ.このとき線形変換\( \, DF \, \)の表現行列
\[
\begin{pmatrix} \frac{ \partial f }{ \partial x } ( x_{0}, y_{0} ) & \frac{ \partial f }{ \partial y } ( x_{0}, y_{0} ) \\ \frac{ \partial g }{ \partial x } ( x_{0}, y_{0} ) & \frac{ \partial g }{ \partial y } ( x_{0}, y_{0} ) \end{pmatrix}
\]
を\( \, \begin{pmatrix} x_{0} \\ y_{0} \end{pmatrix} \in \mathbb{ R }^{2} \, \)における\( \, F \, \)のヤコビ行列(Jacobian matrix)という.
証明の詳細に関してはこちらを参照して頂きたいのですが、概略を説明します。
\( \, F( x, y ) \, \)は\( \, \begin{pmatrix} x_{0} \\ y_{0} \end{pmatrix} \in \mathbb{ R }^{2} \, \)において微分可能だから任意の\( \, \varepsilon > 0 \, \)に対して、ある\( \, \delta > 0 \, \)が存在して
\[
\sqrt{ ( x \ – \ x_{0} )^{2} + ( y \ – \ y_{0} )^{2} } < \delta
\]
ならば
\[
\begin{align*}
\left | \frac{1}{ \sqrt{ ( x \ – \ x_{0} )^{2} + ( y \ – \ y_{0} )^{2} } } \left ( \begin{pmatrix} f( x, y ) \\ g( x, y ) \end{pmatrix} \ – \ \begin{pmatrix} f( x_{0}, y_{0} ) \\ g( x_{0}, y_{0} ) \end{pmatrix} \ – \ DF \begin{pmatrix} x \ – \ x_{0} \\ y \ – \ y_{0} \end{pmatrix} \right ) \right | < \varepsilon
\tag{1}
\end{align*}
\]
が成り立ちます。ここで \( \, y = y_{0} \, \)とおくと
\[
\sqrt{ ( x \ – \ x_{0} )^{2} } = | x \ – \ x_{0} | < \delta
\]
ならば
\[
\left | \frac{1}{ x \ – \ x_{0} } \left ( \begin{pmatrix} f( x, y_{0} ) \\ g( x, y_{0} ) \end{pmatrix} \ – \ \begin{pmatrix} f( x_{0}, y_{0} ) \\ g( x_{0}, y_{0} ) \end{pmatrix} \ – \ DF \begin{pmatrix} x \ – \ x_{0} \\ 0 \end{pmatrix} \right ) \right | < \varepsilon
\]
が成り立ちます。\( \, DF \, \)の線形性により
\[
DF \begin{pmatrix} x \ – \ x_{0} \\ 0 \end{pmatrix} = ( x \ – \ x_{0} ) DF \begin{pmatrix} 1 \\ 0 \end{pmatrix}
\]
となるから
\[
DF \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} a_{11} \\ a_{12} \end{pmatrix}
\]
とおいて成分ごとに計算すれば
\[
\begin{align*}
& \left | \frac{1}{ x \ – \ x_{0} } ( f( x, y_{0} ) \ – \ f( x_{0}, y_{0} ) \ – \ a_{11} ( x \ – \ x_{0} ) ) \right | < \varepsilon
\\
& \left | \frac{1}{ x \ – \ x_{0} } ( g( x, y_{0} ) \ – \ g( x_{0}, y_{0} ) \ – \ a_{12} ( x \ – \ x_{0} ) ) \right | < \varepsilon
\end{align*}
\]
が成り立ちます。したがって \( \, f( x, y ), \, g( x, y ) \, \)は\( \, \begin{pmatrix} x_{0} \\ y_{0} \end{pmatrix} \in \mathbb{ R }^{2} \, \)において \( \, x – \, \)方向に偏微分可能で
\[
a_{11} = \frac{ \partial f }{ \partial x } ( x_{0}, y_{0} ), \quad a_{12} = \frac{ \partial g }{ \partial x } ( x_{0}, y_{0} )
\]
すなわち
\[
DF \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} \frac{ \partial f }{ \partial x } ( x_{0}, y_{0} ) \\ \frac{ \partial g }{ \partial x } ( x_{0}, y_{0} ) \end{pmatrix}
\]
が成り立ちます。
一方、式 \( \, (1) \, \)において \( \, x = x_{0} \, \)とおけば同様にして
\[
DF \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} \frac{ \partial f }{ \partial y } ( x_{0}, y_{0} ) \\ \frac{ \partial g }{ \partial y } ( x_{0}, y_{0} ) \end{pmatrix}
\]
が成り立ちます。
まとめ
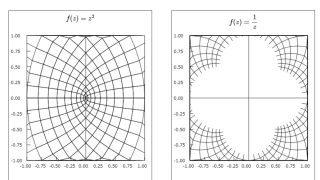
複素解析の本の中の等角写像の節を読んでいたらヤコビ行列という言葉が出てきたので、ヤコビ行列に関する記事をドキュメントにしました。
この記事に記載されている「ε-δ論法」に関してはこちらの記事も参照して頂けると参考になると思っています。
次回は等角写像に関する記事を書こうと考えているところです。


































コメント